Functions reference

Functions help perform actions with values in expressions, this page documents the predefined functions to help with a variety of tasks.

Logic Functions

These functions are useful for building conditional logic into expression results.

They are paired with 2 constant values true and false to represent positive and negative logic signals, mostly used for testing your expressions behave as you expect.

Values evaluate to true if they result in a non-zero result. That is, only 0 evaluates to false. Comparison operators return true or false as expected from their mathematical definitions.

if - Conditional evaluation

Usage: if(cond, if_true, if_false)

• cond (boolean) : The value to check
• if_true (anything) : The value to return if cond is true
• if_false (anything) : The value to return if cond is false

Evaluates the condition cond and returns one of the 2 following values, depending on if it evaluates to true or not.

For example, this function can be used as a part of a larger expression to ‘switch’ between different values. For example if(osc:myaddr > 0, osc:myaddr, self) only allows the animated values in a layer if the value at OSC address /myaddr is greater or equal to 0.

The graph shows the result of if(x > 0.5, 1, -1)

and - Logical AND operation

Usage: and(x, y)

• x (number) : The first value to check
• y (number) : The second value to check

Returns 1 if both x and y test as true.

The graph shows the result of and(x, 1)

or - Logical OR operation

Usage: or(x, y)

• x (number) : The first value to check
• y (number) : The second value to check

Returns 1 if either x or y test as true, or both.

The graph shows the result of or(x, 0)

step - Activation function

Usage: step(x, y)

• x (number) : The first value to compare
• y (number) : The second value to compare

Returns 1 if x >= y, otherwise returns 0.

Can be used as a part of a larger expression to ‘turn on’ a source of data. For example step(osc:myaddr, 0.5) * self only allows the animated values in a layer if the value at OSC address /myaddr is greater or equal to 0.5.

The graph shows the result of step(x, 1)

Trigonometric functions

These functions are useful for working with angles and geometry.

A predefined constant pi contains the value of PI, approximately 3.14159.

sin - Trigonometric sine

Usage: sin(x)

• x (radians) : The angle to convert

Returns the sine of the given angle

cos - Trigonometric cosine

Usage: cos(x)

• x (radians) : The angle to convert

Returns the cosine of the given angle

tan - Trigonometric tangent

Usage: tan(x)

• x (radians) : The angle to convert

Returns the tangent of the given angle

asin - Trigonometric arcsine

Usage: asin(x)

• x (sine) : The sine to convert

The arcsine, or inverse of sine. Converts from the sine of an angle (x) to the initial angle, measured in radians.

The sine of an angle can be thought of as the y coordinate of a point on the circumference of a unit circle.

acos - Trigonometric arccosine

Usage: acos(x)

• x (cosine) : The cosine value to convert

The arccosine, or inverse of cosine. Converts from the cosine of an angle (x) to the initial angle, measured in radians.

The cosine of an angle can be thought of as the x coordinate of a point on the circumference of a unit circle.

atan - Trigonometric arctangent

Usage: atan(x)

• x (tangent) : The tangent value to convert

The arctangent, or inverse of tangent. Converts from the tangent of an angle (x) to the initial angle, measured in radians.

atan2 - Trigonometric arctangent (2-argument variant)

Usage: atan2(x, y)

• x (distance) : The position along the X axis to build an angle from
• y (distance) : The position along the Y axis to build an angle from

This is equivalent of atan(y / x), but in the case where x is 0 or either values could be negative, this provides an accurate angle.

The graph shows the result of atan2(x, -4)

This function is useful to determine the angle between two objects on the plane of a given axis.

radians - Convert from degrees to radians

Usage: radians(x)

• x (degrees) : The angle to convert

This converts from degrees to radians, which is then suitable for use in the above functions.

The conversion is a linear function - simply multiply by pi / 180.

degrees - Convert from radians to degrees

Usage: degrees(x)

• x (radians) : The angle to convert

This converts from radians to degrees, which is then suitable for displaying to humans who are used to working in degrees.

The conversion is a linear function - simply divide by pi / 180.

Mathematical functions

exp - Exponent

Usage: exp(x)

• x (number) : The exponent

Raise e (Euler’s number, approximately equal to 2.71828) to the power of x. Note e is also a constant in disguise expressions.

log - Natural logarithm

Usage: log(x)

• x (number) : The value

Takes the logarithm of the input number x against the base e. This means this is the inverse of exp.

log10 - Base 10 logarithm

Usage: log10(x)

• x (number) : The value

Takes the logarithm of the input number x against the base 10. This can be used to get the number of digits after the most significant number (e.g. log10(1000) returns 3.)

sqrt - Square root

Usage: sqrt(x)

• x (number) : The value

Returns the value which, when multiplied by itself, results in the input.

pow - Power function

Usage: pow(x, y)

• x (number) : The base
• y (number) : The exponent

Returns a value which is x raised to the power of y. To implement exp, one would write pow(e, x).

abs - Absolute value

Usage: abs(x)

• x (number) : The signed value

Returns the absolute (positive) number, no matter the sign of the input value.

floor - Rounding down

Usage: floor(x)

• x (number) : The value

Returns the input value, rounded down to the integer value below it.

ceil - Rounding up

Usage: ceil(x)

• x (number) : The value

Returns the input value, rounded up to the integer value above it.

max - Maximum value

Usage: max(x, y)

• x (number) : A candidate value
• y (number) : A candidate value

Returns the maximum of the 2 inputs provided.

The graph shows the result of max(x, 2)

min - Minimum value

Usage: min(x, y)

• x (number) : A candidate value
• y (number) : A candidate value

Returns the minimum of the 2 inputs provided.

The graph shows the result of min(x, 2)

clamp - Restrict within the given range

Usage: clamp(x, min, max)

• x (number) : The value to clamp
• min (number) : The minimum bounds of the operation
• max (number) : The maximum bounds of the operation

Returns the input value x if it is between min and max, otherwise it remains at those values.

The graph shows the result of clamp(x, -1, 2)

lerp - Remap a value to a new range

Usage: lerp(low, high, amount)

• low (number) : The value returned when amount is 0
• high (number) : The value returned when amount is 1

When amount is between 0 and 1, the function returns some fraction between low and high. When amount is outside the range of 0 and 1, the function linearly interpolates outside the range of low and high.

The graph shows the result of lerp(2, 4, x)

Integer operations

Normal operators like % and / are performed using floating point. This means for example that 3 / 2 would result in approximately 1.5.

However there are cases where we want to consider the operations in terms of whole numbers.

% - Remainder operator

Usage: x % y

• x (number) : The numerator
• y (number) : The denominator

Operator for getting the remainder after integer division of two numbers (e.g. 5 % 2 == 1)

The graph shows the result of x % 2

int - Integer conversion

Usage: int(x)

• x (number) : The number to convert

Returns a rounded-down version of the input value. This is equivalent to floor.

idiv - Integer division

Usage: idiv(x, y)

• x (number) : The numerator
• y (number) : The denominator

Returns an integer version of the numerator divided by an integer version of the denominator, returning an integer value.

The graph shows the result of idiv(x, 2)

Resource access function

getByUID - Resource access

Accessing properties from Resources in the system is a very powerful method for enhancing expressions. Referencing resources is normally performed by name. However, it’s possible to refer to Resources by UID instead. This allows for a strong reference to the original Resource, at the expense of readability. The benefit of this less readable approach is that the reference remains even if the Resource (e.g. a Layer) is renamed. Expressions are not updated in response to rename operations. This is described further in Accessing Resources by UID.

A user will right-click the title bar of a Resource editor, and select Copy UID. They will then paste that UID as the argument of this function.

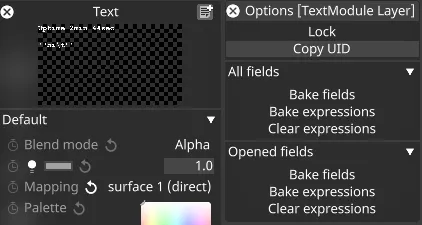
For example: getByUID(0x123456789012345).description returns the name of the Resource the user right-clicked on.

The set of properties on Resources is subject to change. See Accessing Resources for more information.